Лабы
Модель нейрона
Нейрон представляет собой единицу обработки информации в нейронной сети.
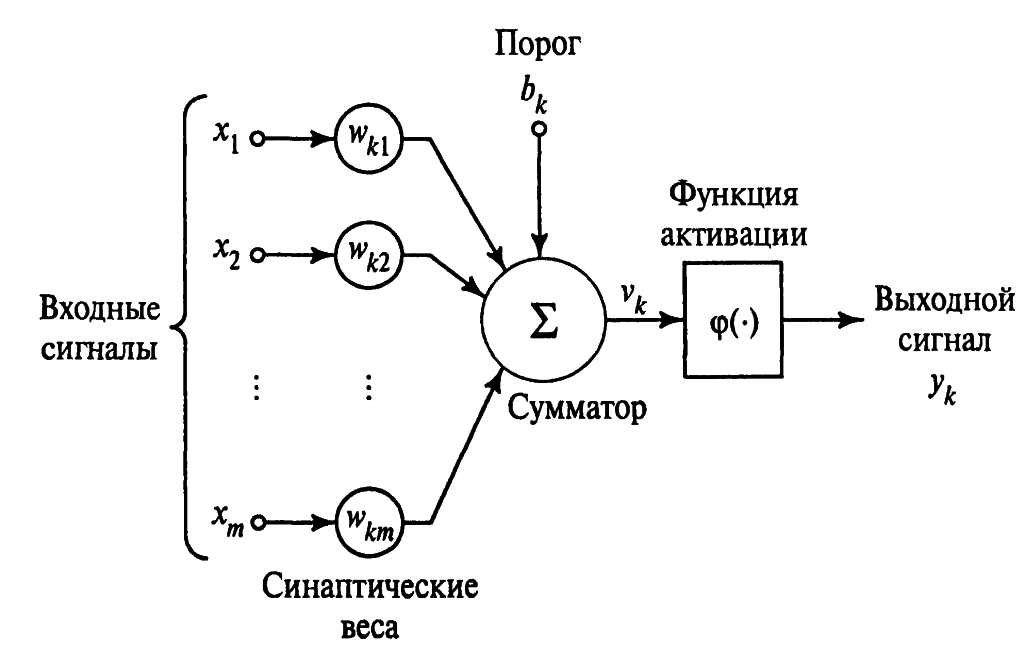
Выше показана модель нейрона, лежащего в основе искусственных нейронных сетей. В этой модели можно выделить три основных элемента:
- Набор синапсов (synapse) или связей (connecting link), каждый из которых характеризуется своим весом (weight) или силой (strength). В частности, сигнал $x_j$ на входе синапса $j$, связанного с нейроном $k$, умножается на вес $w_{kj}$. Важно обратить внимание на то, в каком порядке указаны индексы синаптического веса $w_{kj}$.Первый индекс относится к рассматриваемому нейрону, а второй – ко входному окончанию синапса, с которым связан данный вес. В отличие от синапсов мозга синаптический вес искусственного нейрона может иметь как положительные, так и отрицательные значения.
- Сумматор (adder) складывает входные сигналы, взвешенные относительно соответствующих синапсов нейрона. Эту операцию можно описать как линейную комбинацию.
- Функция активации (activation function) ограничивает амплитуду выходного сигнала нейрона. Эта функция также называется функцией сжатия (squashing function). Обычно нормализованный диапазон амплитуд выхода нейрона лежит в интервале $[0, 1]$ или $[-1, 1]$.
В представленную модель нейрона включен пороговый элемент (bias), который обозначен символом $b_k$. Эта величина отражает увеличение или уменьшение входного сигнала, подаваемого на функцию активации.
В математическом представлении функционирование нейрона $k$ можно описать следующей парой уравнений:
$u_k = \sum_{j=1}^m w_{kj} x_j$ (1)
$y_k=φ(u_k+b_k)$ (2)
Типы функций активаций
Функции активации, представленные в формулах как $φ(v)$, определяют выходной сигнал нейрона в зависимости от индуцированного локального поля $v$. Можно выделить три основных типа функций активации.
- Функция единичного скачка, или пороговая функция (threshold function). Этот тип функции описывается следующим образом: $φ(v) = \begin{cases} 1, & если \, v ≥ 0 \\\\ 0, & если \, v < 0 \end{cases}$
- Кусочно-линейная функция (piecewise-linear function). Описывается следующим выражением: $φ(v) = \begin{cases} 1, & если \, v≥ + \frac 12 \\\\ |v|, & если \, -\frac 12 < v < +\frac 12 \\\\ 0, & если \, v ≤ -\frac 12 \end{cases}$
- Сигмоидальная функция (sigmoid function). График напоминает букву S, функция является, пожалуй, самой распространенной функцией, используемой для создания искусственных нейроных сетей. Примером сигмоидальной функции может служить логистическая функция, задаваемая следующим выражением: $φ(v) = \frac{1}{1+exp(-av)}$ где $a$ – параметр наклона сигмоидальной функции.
Задание 🔔
- Реализовать искусственный нейрон с двумя входами, описанный формулами (1) и (2) в виде класса. Использовать пороговую функцию активации.
- Подобрать веса ($w_{kj}$) и смещение $b_k$ нейрона для решения задачи по варианту. Значения можно задать в коде класса или передавать в качестве агрумента при создании объекта.
- В основном теле программы создать объект класса
Neuronи продемонстрировать его корректную работу.
import numpy as np
class Neuron:
weight : np.ndarray[float] # Можете сразу задать веса
bias : float # и смещение.
def __init__(self, w: np.ndarray[float] = None, b: float = None):
if w: # Или можете
self.weight = w # задать веса
if b: # и смещение
self.bias = b # при инициализации.
def _threshold_function(self, x: np.ndarray[float]) -> int:
pass
def predict(self, x: np.ndarray[int]) -> int:
u = 0
# Ваш код (умножить входы на веса и просуммировать).
return self._threshold_function(u + self.bias)
| Вариант | Входные данные | Выходные данные | Название булевой функции |
|---|---|---|---|
| 1 | 0 0 0 1 1 0 1 1 |
0 0 0 1 |
Коньюнкция |
| 2 | 0 0 0 1 1 0 1 1 |
1 0 1 1 |
Обратная импликация |
| 3 | 0 0 0 1 1 0 1 1 |
1 1 0 1 |
Импликация |
| 4 | 0 0 0 1 1 0 1 1 |
0 0 1 0 |
Инверсия прямой импликации |
| 5 | 0 0 0 1 1 0 1 1 |
1 0 0 0 |
Стрелка Пирса |
| 6 | 0 0 0 1 1 0 1 1 |
1 1 1 0 |
Штрих Шеффера |
Пример дизъюнкции
0 0 1 1 $x_1$ ($\overrightarrow{w_{11}=1}$)
$\,\,\,\,\,\,\,\,\,\,\,\,φ(v) = \begin{cases} 1 & если \, x>0 \\\\ 0 & если \, x≤0 \end{cases}\,\,\overrightarrow{w_{21}=1}\,\,$ y = 0 1 1 1
0 1 0 1 $x_2$ ($\overrightarrow{w_{12}=1}$)