Лабы
Однослойная сеть
Градиентный спуск и Правило обучения Уидроу-Хоффа. Обучение однослойной нейронной сети
Читаем cтр. 16 – 24. в учебном пособии Гафаров Ф.М. Искусственные нейронные сети и приложения.
Пояснения к заданию 1:
Слой нейронной сети, состоящий из нескольких нейронов можно было бы представить в виде списка объектов класса Neuron из прошлой лабораторной. Но значительно лучше переходить массивам numpy, потому что это будет проще и быстрее.
где $n$ - количество входов, $m$ - количество нейронов в слое.
Шаг 1
Создать класс полносвязной однослойной нейронной сети с возможностью произвольного задания количества нейронов и произвольного количества входов нейронов. Добавить инициализацию значений весов случайными малыми значениями $[0.001; 0.2]$. Функцию активации использовать линейную.
import numpy as np
class NeuralNetwork:
weight : np.ndarray
bias : np.ndarray
def __init__(self, n: int, m: int):
pass
def _activation_function(self, x: np.ndarray) -> int:
pass
def predict(self, x : np.ndarray) -> np.ndarray:
pass
def fit(self, x : np.ndarray, y : np.ndarray):
pass
Шаг 2. Первый вариант обучения
Нейрон с двумя входами и линейной функцией активации: $y = 3x_1 + 2x_2$
Данные для обучения:
| № | $x_1$ | $x_2$ | y |
|---|---|---|---|
| 1 | 1 | 3 | 8 |
| 2 | 2 | 4 | 11 |
| 3 | 1 | 5 | 9 |
| $n$ | .. | .. | .. |
Расчет ошибки предсказания для первого примера:
$y_{1pred} = 3 * 1 + 2 * 3 = 9$
$ε = 1$
$(3 + Δ_1) * 1 + (2 + Δ_1) * 3 = 8$
$4Δ_1 = 8 - 9$
$Δ_1 = -0.25$
Нейрон с обновленными весами: $y = 2.75x_1 + 1.75x_2$
Формула для обновления весов нейронов (для NeuralNetwork.fit_1()):
$ ω_{ij}^{t+1}=ω_{ij}^t + \frac {y_{ki} - \sum_{j=1}^n ω_{ij}^t x_{kj}}{\sum_{j=1}^n ω_{ij}^t },$ (1)
где $t$ - номер шага обучения, $k$ - номер обучающего примера, $i$ - номер нейрона в слое, $j$ - номер входа.
Шаг 3. Второй вариант обучения
Аналитическое решение (математические формулы) – это идеально, если оно есть. В случаях, когда красивой формулы нет или она есть, но ее надо представить в виде программного кода, мы обращаемся к вычислительной математике.
Надо понимать, что машинные числа являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера, следовательно, неизбежно падает точность.
Оптимизация подразумевает нахождение экстремума целевой функции, когда заданы переменные (что можно изменять) и ограничения (какие условия должны обязательно выполняться). Большинство численных методов оптимизации – итеративные: в цикле определяется новое значение $X$ (предположительно, приближающееся к глобальному экстремуму), для которого рассчитывается значение $Y$. Критерием останова для них является момент, когда изменение значения функции за шаг становится меньше заданной точности ε.
Методы оптимизации. Градиентный спуск.
Как нам известно, градиент – вектор, указывающий направление наискорейшего роста некоторой скалярной величины. Поэтому, чтобы найти минимум функции, нам надо двигаться в сторону антиградиента (это все при условии, что нам известна формула, выражающая функцию, и она дифференцируема).
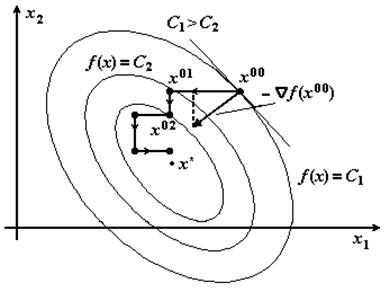
$\bar x ^{k+1} = \bar x^k - α∇Φ(\bar x^k )$, (2)
где $∇Φ(\bar x) = \left(\begin{matrix} \frac {∂Φ}{∂x_1} \\ \frac {∂Φ}{∂x_2} \\ .. \\ .. \end{matrix} \right) $ ,
$α$ – задаваемый шаг, лучше делать меньше 0.01.
В случае обучения нейронной сети, оптимизируемая функция – функция ошибки обучения. Пусть будет среднеквадратичная ошибка:
$E=\frac 12 (y-y_{расчетный} )^2$ (3)
Подставив в формулу (2) вес c индексом (вместо вектора) и оптимизируемую функцию, получим:
$ω_{ij}^{t+1} = ω_{ij}^t - α \frac {∂(\frac 12 ( \sum_{j=1}^n f(ω_{ij}^t x_{j})-y_i)^2}{∂x_j},$
где $t$ - номер шага обучения, $i$ - номер нейрона в слое, $j$ - номер входа.
В случае линейной функции активации $f$, производная считается легко.
Получаем формулу для обновления весов нейронов (для NeuralNetwork.fit_2()):
$ω_{ij}^{t+1} = ω_{ij}^t - α \left( \sum_{j=1}^n (ω_{ij}^t x_{kj} - y_{ki}) * x_{kj} \right), $ (4)
где $k$ - номер обучающего примера.
Или в векторном виде:
$ W^{t+1} = W^t - α (W^t \times x - y) \times x^T, $
где $W$ - матрица весовых коэффициентов, $t$ - номер шага обучения, $x$ - вектор-столбец входных значений, $y$ - вектор-столбец выходных значений, $v^T$ - операция транспонирования.
Шаг 4
За один проход ничего не обучится, поэтому реализуем в методе fit() последовательность шагов при обучении однослойной нейронной сети по правилу обучения Уидроу-Хоффа:
- Задаются шаг обучения $α (0 < α < 1)$ и желаемая среднеквадратичная ошибка сети $E_m$.
- Инициализируются случайным образом весовые коэффициенты $w_{i,j}$ и пороговые $b_j$ значения нейронов.
- Подаются последовательно образы из обучающей выборки на вход нейронной сети. Вычисляется выходные значения нейронов.
- Производится изменение весовых коэффициентов и порогов нейронных элементов.
- Вычисляется суммарная ошибка нейронной сети $E$.
- Если $E>E_m$, то происходит переход к шагу 3, иначе выполнение алгоритма завершается.
Задание 1
- Выполняем шаги 1-4.
- В теле программы создаем 2 одинаковых сети из одного нейрона с двумя входами. Одна из сетей будет обучаться по формуле (1), вторая – по (4).
- Берем файл с данными. Это координаты точек, принадлежащих плоскости $y=3x_1-2x_2.$ Будем обучать предсказывать $y$ по $x_1$ и $x_2.$
- Самостоятельно делим выборку на обучающую (80%) и тестовую (20%). НЕ используя готовые библиотеки.
- Обучаем 2 нейронные сети на обучающей выборке.
- Считаем среднеквадратичную ошибку (3) на тестовой выборке.
- Смотрим, какие веса получились.
Задание 2
В теле программы создаем сеть из 3-х нейронов. У каждого нейрона 6 входов. Обучаем нейронную сеть на данных из файла 2lab_data.csv.
Задание 3
Обучаем сеть распознавание красного цвета на картинке:
- Обучаем сеть из 1 нейрона с 3 входами (RGB) на обучающей выборке. Смотрим точность на тестовой выборке. Если не обучается, попробуйте подобрать веса вручную.
- Смотрим результат на картинке из которой брались пиксели для обучения. Можно самостоятельно или используя код ниже.
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
a = np.asarray(Image.open('pic.jpg'))
mas = a.reshape(1920*1080,1,3)
res = []
for i in range(len(mas)):
res.append(100 * your_precious_NeuralNetwork.predict(mas[i]))
plt.figure(figsize=(15.,10.))
plt.imshow(Image.fromarray(our_array, mode="L"))