Multihead

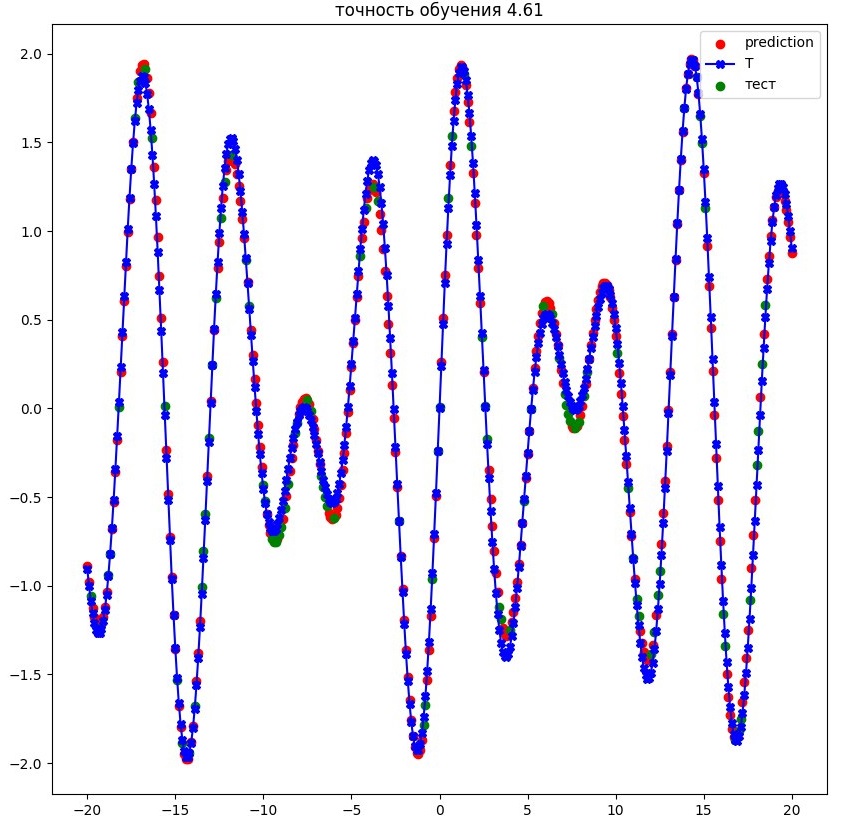
Используя библиотеку Keras на Python мы будем обучать нейронную сеть, аппроксимирующую функцию $f(x) = sin(x)+sin( \sqrt{2} x)$, которая представлена на рис. ниже.

Задание

Шаг 1

Создать набор данных на две колонки: $X$ от -20 до 20 с шагом 0.1 и $Y=f(x)$.
Скопировать код:

# Разделить на обучающую и тестовую выборки.
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=13)

# Обучить с указанными параметрами.
model.compile(loss='mse', optimizer='rmsprop', metrics=['mae'])
model.fit(X_train, y_train, epochs=150, batch_size=10)

# Посчитать и вывести точность на обучающем и тестовом наборах данных.
_, accuracy = model.evaluate(X_train, y_train)
_, accuracy2 = model.evaluate(model.predict(X_test), y_test)

Вывести график функции и точек предсказания нейронки на тестовом наборе.
Сравнить с рис. выше. Точность обучения - это accuracy * 100.
Подобрать наиболее простую архитектуру сети (количество слоев, количество нейронов в слоях, функции активации), которая обеспечивает близкую точность.

Шаг 2

Знание о периодичности нашей функции (одни и те же значения повторяются через каждые $2\pi$ единиц $x$) позволяет увидеть, как можно облегчить нейронной сети жизнь.

Выделить из функции две переменные: номер периода ($T$) и смещение внутри периодически повторяющегося участка кривой ($\varphi$).
Обучить сеть по двум входам ($T$, $\varphi$) предсказывать один выход ($Y$).
Подобрать наиболее простую архитектуру сети, которая обеспечивает достаточную ($< 15$) точность. Сравнить с предыдущим вариантом.

Шаг 3

То, что мы увидели периодичность и вручную выделили нужные переменные из исходной - это хорошо, но можно ли и эту часть обработки данных переложить на нейронную сеть?

Обучить три сети и объединить:
- Создать две отдельные сети, которые будут извлекать значения периода и смещения из исходной переменной. Первая сеть обучается по $x$ предсказывать $T$, вторая - $x$ → $\varphi$.
- Подобрать архитектуры, хорошо обучить.
- Объединить три предварительно обученные сети ($^1 x → T$, $^2 x → \varphi$, $^3 (T, \varphi) → Y=f(x)$) в одну сложную. Вывести результат.
Сначала объединить три сети в одну сложную. Затем обучить. Вывести результат.
Сравнить с предыдущими решениями.

Принимаются идеи улучшения, альтернативные решения, и объяснения, почему рассмотренное работает так, как оно работает.